Jayne Overgard
Math 696
HW#3 problem 1a.
| > | f:=exp(.1*x)*sin(x); for n from 1 to 6 do p:=NULL; for n from 1 to 6 do g:=convert(taylor(f,x=0,n),polynom); p:=p,g;od; plot([f,p],x=-5..5); p:=p,g; end do; |
![]()
![]()
![[Maple Plot]](images/math696HW33.gif)
![]()
![]()
HW#3 problem 1b.
| > | restart; m:=exp(.1*x)*sin(x); n:=convert(taylor(m,x=a,6),polynom); unassign(a); |
![]()
![]()
![]()
![]()
| > |
HW#3 problem 2a.
| > | f := proc( a, b ) local primes,p,numprimes,i; primes:= {}; numprimes := 0; for i from a to b do i:= nextprime(i); primes := primes union {i}; numprimes := numprimes + 1 end do; print("Finding the twin prime pairs in the interval."); for i from 2 to numprimes-1 do if primes[i] - primes[i-1] = 2 then print(primes[i-1],primes[i]) end if; end do; end proc: |
| > | print("Type in f(a,b) where a and b is an interval. End with ; and then enter"); |
![]()
| > | f(1,60); |
| > |
![]()
![]()
![]()
![]()
![]()
![]()
| > |
| > |
HW#3 problem 2b.
| > | g := proc( a, b ) local primes,p,numprimes,i,numtwins; primes:= {}; numprimes := 0; for i from a to b do i:= nextprime(i); primes := primes union {i}; numprimes := numprimes + 1 end do; numtwins := 0; for i from 2 to numprimes-1 do if primes[i] - primes[i-1] = 2 then print(primes[i-1],primes[i]); numtwins := numtwins + 1 end if; end do; print(`Number of twin pairs is: `); print(numtwins); end proc: print("Finding the twin prime pairs in the interval."); print("Type in g(a,b) where a and b is an interval. End with ; and then enter"); |
| > |
![]()
![]()
| > | g(1,60); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > |
| > |
| > | restart; |
HW#3 problem 3
| > | r := proc(c,d) local a, n, countprimes; countprimes :=0; if gcd(c,d) = 1 then for n from 1 to 100 do a := c + n*d; if type(a, prime) then countprimes := countprimes + 1; print (a) end if; end do; else print("Those two numbers are not relatively prime. Please try again."); end if; print("The number of primes is:"); print(countprimes); end proc: |
| > | print("Please enter r(c,d) substituting c,d with integers. End with ; then enter."); |
![]()
| > | r(3,501); |
![]()
![]()
![]()
| > | r(3,5); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > |
| > |
| > | restart; |
HW#3 problem 4.
| > | with(LinearAlgebra): h :=proc(n) local y,z,i; y := HilbertMatrix(n); printf("\nHilbert Matrix\n"); print(y); printf("\nMatrix Inverse\n"); print(MatrixInverse(y)); printf("\nDeterminant\n"); print(Determinant(y)); printf("\nConditional Number\n"); print(ConditionNumber(y)); printf("\nPrinciple Submatrices\n"); for i from 2 to n-1 do z := HilbertMatrix(i); printf("\nSubmatrix %dx%d\n",i,i); print(z); printf("\nComputed %dx%d determinant is:\n",i,i); print(Determinant(z)); end do; end proc: |
| > |
Please enter h(n) of your choice to generate a Hilbert matrix of size n.
End with ; and enter.
| > | h(4); |
Hilbert Matrix

Matrix Inverse

Determinant
![]()
Conditional Number
![]()
Principle Submatrices
Submatrix 2x2
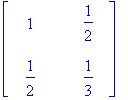
Computed 2x2 determinant is:
![]()
Submatrix 3x3

Computed 3x3 determinant is:
![]()
| > |